Recently, I came across the following problem, I had a dataset from which I had to predict its class, this class was not binary, that is, it was a set of categories, until here everything normal, but, later I noticed that in fact the dataset not only have one class but three and none of them were binary, well, well, I found a dataset in the UCI repository that explain this problem better. Click to download here.
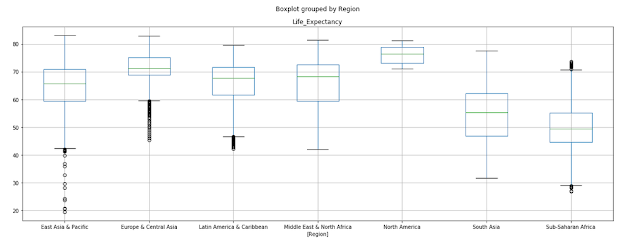
Basically the dataset contains 22 numerical fields that represent measurements of the sound that some species of frogs do, this dataset has three categories to classify: Families, Genus and Species, each of these, in turn, are multi-classes and its data are:
Families
- Bufonidae
- Dendrobatidae
- Hylidae
- Leptodactylidae
Genus
- Adenomera
- Ameerega
- Dendropsophus
- Hypsiboas
- Leptodactylus
- Osteocephalus
- Rhinella
- Scinax
Species
- AdenomeraAndre
- AdenomeraHylaedact
- Ameeregatrivittata
- HylaMinuta
- HypsiboasCinerascens
- HypsiboasCordobae
- LeptodactylusFuscus
- OsteocephalusOopha
- Rhinellagranulosa
- ScinaxRuber
And this is where things become interesting, for the same entry we will have three labels, to say: familie, genus and Species which we will have to classify, and each of these labels contain several categories, so how do we work with these datasets?
In this post I will explain step by step how to work with these data sets, I will use the python language for practicality, however, I will explain how this algorithms works, so they can be implemented in the language of your preference.
First we import the libraries that we will use:
Now, we will create a function that will receive a classifier 'x', training data , testing data and we will return its performance
Now we will load and study our dataset (for those who do not know python, the .head () method prints the first 5 rows)
As we can see our data set consists of 7195 rows and 26 columns, of which 3 of them are our labels and the others are our data, all of them numerical, we can see that we do not have to do much about cleaning it, in fact, only I will convert the columns classes into categories to improve the performance a bit.
Well, the next step will be to convert each class into a binary column so that the algorithms can work
The same with the others two classes
Concat the dataframes
Let's separate the original dataframe into two dataframes, that is, one that represents the data and another the classes
Now we generate the training and testing data sets
Now what ?, well, we can not use any algorithm here because it failed miserably, since we have a problem of multilabel, that is, we have to classify here three classes instead of one, let's see an example of how any algorithm would fail
Then what do we do? , well we have three ways to deal with these kind of problems:
- - Binary Relevance
- - Classifier Chains
- - Label Powerset
Binary Relevance:
This is the divide and conquer, basically it takes each possible class individually and classify it, then concatenate everything and get the result:
Original:
Transforms it into:
Classifier Chains
This technique first takes only one class column and classifies it, then it takes another class column to classify it but the first will be part of the data, then it will take a third and the first two will be part of the data, ufff, the follow image shows better this process.
Original :
Transforms it into:
The data shaded in yellow are what we would use to classify our class
Label Powerset
In my opinion the most simple to understand, here we try to label the different conditions in which the classes are generated and we create new classes
Original :
Transforms it into:
This method is the simplest, however, it is worth mentioning that we would need to have all possible combinations to generate all possible classes
Which method is better? Well, sincerely it is better to experiment all the cases to see which one fits our problem, for python we have that the skmultilearn.problem_transform library gives us these methods.
As we observed, at least for this dataset, the techniques that fits better were Chain and Label PowerSet
The complete code can be downloaded here